|
Kangaroos use their front legs, back legs, and tail to propel themselves at speeds of up to 44 mph and are the only known animal to be classified as pentapods. Inspired by this interesting pentapedal motion, my team set out to design and build a robot that would mimic the five-legged walking of real kangaroos.
|
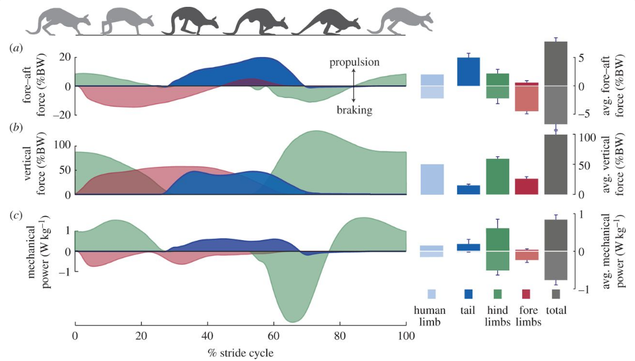
The provided specs required that the robot kangaroo could be no more than 20 cm long and had to propel itself at a speed of at least 10 cm/s. Karen’s gait had to resemble the actual gait of kangaroos, which is analyzed in the diagram below by O’Connor et al. The middle graph reveals when different appendages are on the ground. When the kangaroo’s hind limbs lift, the tail steps in to stabilize the kangaroo.
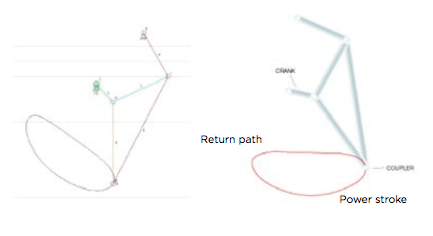
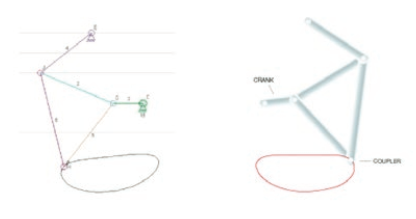
We used two four-bar linkage designs: one for the front legs and one for both the hind legs and tail. We chose linkages loosely modeled after the Hoeken’s Linkage, with quick return paths and slower power strokes. Because a kangaroo’s hind legs and tail are in contact with the ground for longer than their front legs, the power stroke of Linkage 1 has a larger radius of curvature than that of Linkage 2.
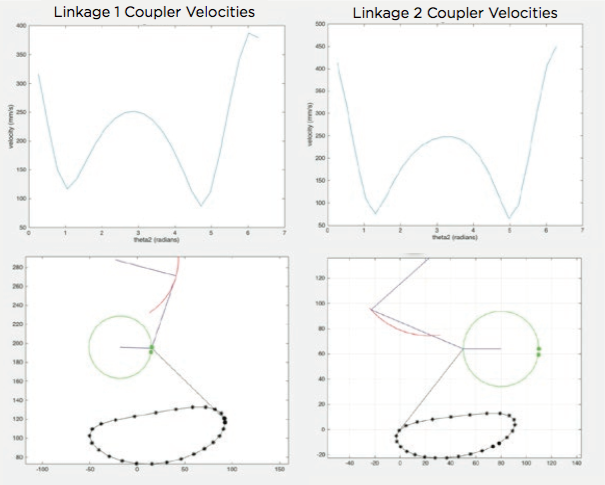
After modeling the linkages, we created a MATLAB program that analyzed coupler velocities. We then calculated that each mechanism’s maximum contact velocity of 25 cm/s would require roughly .64 W of power from the motor.
|
To power our kangaroo, we replaced mitochondria with a 6-speed motor that allowed us to customize its gear train. We designed the motor to have a gear ratio of 196.7 : 1 that would give us enough torque to push Karen off the ground. The motor was powered with 3.2 V through two AA batteries.
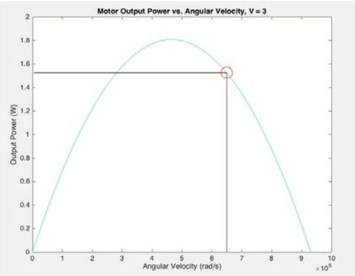
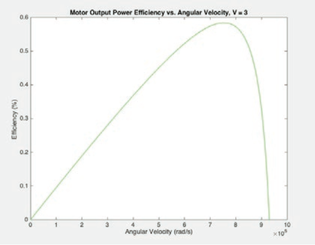
With an internal resistance (R) of 1.11 Ω, a motor constant (k) of 3.045x10^-6 V/rad*s, and a frictional torque (T ) of 4.57x10^-7 N*m, we used MATLAB to characterize the efficiency and output of our motor. |
At an operating angular velocity of 6.7x105 rad/s, the motor operated at about 56% efficiency. At this angular velocity, the motor provided an output power of 1.55 W.
|